

 |
 |
| 首页 > 新闻 > 科研新闻 > 作物 QTL 定位方法研究进展 | 字号选择: |
| 作物 QTL 定位方法研究进展 |
|
早在20世纪20年代,Sax 研究认为菜豆种皮色(单基因质量性状)不同基因型间种子大小(数量性状)的显著差异是由于控制种皮色基因与控制种子大小基因间的连锁造成的.这实质上就是单标记分析。由此,出现了基于标记的性状平均数差异 t 检验法、方差分析法、回归分析法和极大似然法以及基于性状的标记频率差异检验方法.这些方法的缺点是众所周知的。Thoday 提出利用两连锁标记来定位数量性状多基因,此方法的研究结果更为准确。但是,筛选两连锁标记在当时十分困难,限制了它的应用。随着分子生物学的发展,研究人员已获得了许多作物的高密度分子标记连锁图谱,使从整个基因组上定位 QTL 成为可能,Lander 和 Botstein 的区间作图法就应运而生。其主要贡献是建立了 QTL 定位的基本框架,首次实现了在全基因组水平上搜索 QTL,并估计其效应与位置。与区间作图类似的有回归分析法。前者是目标性状对后验概率的回归,后者是对先验概率的回归。若 QTL 在标记附近,两种概率相近,则两方法结果相当;否则,前者优于后者。这纠正了原认为两方法结果均相似的观点。 若同一染色体上有多个连锁的 QTL,用区间作图法会造成待估 QTL 位置与效应估计值的偏差。极端地,若紧密连锁两 QTL 的作用方向相反,往往检测不到;若作用方向相同,在两 QTL 间可能会出现一个“幻影” QTL。当检测多个 QTL 时,因不同 QTL 所用的遗传模型不同,致使其贡献率不能直接相加。即使强行相加,也经常会出现总贡献率远大于100%的情形。为此,Jansen 和 Zeng 独立地提出复合区间作图法。其关键在于怎样选择作为控制遗传背景的协变量——分子标记。标记太多会降低 QTL 检测的功效,太少又达不到控制遗传背景的目的。实质上,该法仍然是单 QTL 模型。为此,Kao 和 Zeng 提出了多区间作图法,其模型中同时包含了多个 QTL 及其两两互作。这是真正意义上的多 QTL 遗传模型,为 QTL 定位开辟了新视野,也体现了 QTL 定位的艺术。 目前,多 QTL 定位的方法主要有极大似然法和 Bayesian 方法两大类。前者包括多区间作图法和惩罚最大似然法,其运算速度较快;后者则主要有可逆跳跃 MCMC (Markov chain Monte Carlo) 方法、Yi 等人提出的方法和压缩估计方法。多区间作图法的不足在于,只能检测具有主效 QTL 间的互作,有时还不能检测到效应较小的 QTL。可逆跳跃 MCMC 的 Bayesian 法的收敛速度太慢,这是 Yi 等人抛弃该方法并提出一种新的 Bayesian 方法的原因。Wu 和 Li 认为,Bayesian 压缩估计方法将 QTL 定位策略推进到利用所有标记的上位性 QTL 的全基因组检测。虽然该法收敛较快,但是它假定的 QTL 数太多致使运算时间太长。为克服这一问题,提出了惩罚最大似然方法。但是,若标记太多,该法的参数估计也是困难的。为此,我们已将可变区间思想同惩罚最大似然方法与 Bayesian 压缩估计方法相结合,以显著减少模型中变量个数。上述方法均是针对某一时间点数量性状观测值(往往为最终结果)的 QTL 定位,即静态 QTL 定位。然而,性状的表达是一个过程。因此,从动态角度定位 QTL 也是重要的。最近,国际上的最新热点是 eQTL 定位,即利用表型观测值、分子标记和表达谱数据定位出控制数量性状的基因。 迄今为止,QTL 定位方法有了长足的发展,已经发展了适合不同倍性(二倍体、三倍体胚乳与同源多倍体)、连续性与间断性(二歧或多歧)变量、静态与动态性状、单一性状与多个相关性状联合、单个组合与多个组合联合以及两个亲本与多个亲本甚至育成品种群体的 QTL 定位方法。本文主要对多 QTL 定位、QTL 精细定位和动态性状的 QTL 定位进行较为详细的介绍。 1 多 QTL 定位 1.1 多区间作图法 若回交群体中某一数量性状受 m 个分别位于标记区间 I1,I2,…,Im 的 p1,p2,…,Pm 处 QTL (Q1,Q2,…,Qm )控制,则第 i 个体数量性状表型值 Yi 可表示为
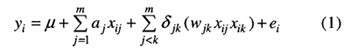 其中,μ为群体平均数;Xij 为 QTL 基因型编码变量,若基因型为 QjQj (或 Qjqj )时,Xij 为1/2(或-1/2);aj 为 QTL 主效;wjk 为两 QTL 间的上位性效应;δjk 为上位性指示变量,存在上位性时取1,否则取0;ei 为服从N(0,δe2 )的随机误差。由此,样本似然函数为
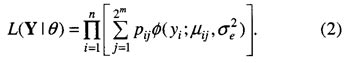 其中,φ(.) 是正态分布密度函数;μij 和 pij 分别是模型(1)中2m 个不同 QTL 基因型值和条件概率。若各 QTL 间相互独立,可通过多点方法计算 pij。 多区间作图法包括4个组成部分:(i)分析特定遗传模型似然的评价程序;(ii)优化遗传模型的搜索策略;(iii)特定模型下各 QTL 位置、主效与互作参数的估计方法;(iV)用于标记辅助选择的个体或子代基因型值的预测模块。中间两过程是关键。对于前者,最初提出用逐步回归;后改为在基础模型上再进行最优模型的确定,此时互作项为 t 项,不是 m(m-1)/2 项。对于后者,Kao 和 Zeng 提出了最大化 lnL(Y|θ)以估计参数的 EM 算法的一般迭代公式。最近,该方法已拓展到间断型性状。 在应用中发现,当无主效 QTL 有互作时,其功效偏低;当 QTL 效应较小时,其功效偏低。这可能是由于在模型拟合开始时误差方差较大所致。若初始模型确定较好,可能会避免该问题。建议联合使用复合区间作图法和双标记互作分析来确定初始模型。但是,若 QTL 位于区间较大的标记中间时,其功效会降低。 1.2 Bayesian 压缩估计方法 Xu 在 Meuwissen 等人的工作基础上,提出了全基因组所有标记联合分析的 Bayesian 压缩估计方法,Zhang 和 Xu 将该法延伸到多 QTL 分析,Wang 等人全面阐述了该方法,Zhang 和 Xu 将它延伸到 QTL 间上位性检测。 模型(1)可变为
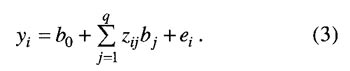 其中,δjk=1,q=m(m+1)/2,b0=μ,bj=aj 和 Zij=xij(j=1,2,…,m),bj+m=wrs 和 zi(j+m)=XirXis (r=1,2,…,m-1;s=r+l,r+2,…,m;j=1,2,…,q-m)。在多标记分析中,假定每标记上存在一个 QTL,m 为标记数目;在多 QTL 分析中,假定每标记区间存在一个 QTL , m为标记区间个数。若假定的 QTL 是假的,则将其效应估计值向0压缩;否则,不压缩。为实现该目标,让每一 QTL (或标记)效应有自己的方差参数,同时该方差有其先验分布,致使每一效应的方差都能从现有资料中估计,以调节效应估计值。其具体作法是假定每一参数有其先验分布,如 p(b0)∝1,p(δe2)∝1/δe2,p(bj)=N(0,δj2) 和 p(δj2)∝1/δj2(j=1,2,…,q);然后,获得每一参数的条件后验分布;例如,bj 是从平均数为 若模型(3)中某 QTL 是假的,从资料中估计的 Braak 等人认为,上述方法的 δj2 先验分布不当并进行了改进。但是,通过比较发现两者效果相差不大。与此相似的还有考虑不同先验方差或平均数的情形。对于前者,Yi 等人和 Oh 等人假定每一效应 bj 服从平均数为0,方差较大和较小的两个正态分布的混合分布,这就是他们独立应用 George 和 McMulloch 的变量选择方法来定位 QTL 的随机搜索变量选择方法。其中,先验方差不从数据中估计而是人为确定。这导致了它比上述压缩估计方法效果差。对于后者,Zhang 等人假定每一效应 bj 服从平均数为正、零和负的3个正态分布的混合分布,提出了 QTL 定位的 Bayesian 分类方法。 1.3 惩罚最大似然方法 针对用上述方法估计互作模型参数的运行时间长的不足,有必要用极大似然方法实现其思想,以节省运行时间。这就是惩罚最大似然方法。遗传模型与模型(3)相同,此时,m为全基因组上标记数。若将所有参数的联合先验分布作为惩罚因子,与似然函数一起构成惩罚似然函数,通过最大化惩罚似然函数就可以估计 QTL 效应及其先验分布参数。应当指出,该方法对参数的先验分布比较敏感,研究发现,下述先验是可行的:p(bo)∝1,p(δe2)∝1/δe2,p(bj)=N(μj,δj2),p(μj)=N(0,δj2/η) 和 p(δj2)∝1。该方法的特点在于各效应的先验平均数与先验方差同各效应一起同时从现有资料中估计。例如,QTL 效应的估计值为
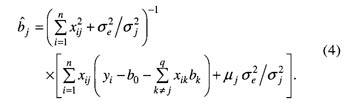 若δj2→0,则 在实际应用时,一种方法是先用惩罚似然方法对所有标记的主效与互作进行分析(这时也可嵌合可变区间的思想以减少模型变量个数),然后用 Bayesian 压缩估计方法进行多 QTL 主效与互作的分析;另一种方法是采取可变区间 Bayesian 压缩估计方法进行多 QTL 主效与互作分析。 2 QTL 精细定位 初步定位 QTL 只说明在某区域可能存在一个控制数量性状的基因,即找到一个基因座,距基因还有一段距离。一方面,QTL 定位的精度还不高,其位置的95%置信区间通常为10~30 cM;另一方面,即使1 cM 的主要农作物 DNA 序列长度至少包括几十万碱基。因此,精细定位 QTL 是应当考虑的。它是指 QTL 位置的95%置信区间为1~5 cM 的 QTL 定位。目前,精细定位 QTL 有3种途径,即发展新的统计方法、增加重组的机会和利用次级分离群体。 Lin 等人在研究高粱开花期遗传时,用区间作图只检测到1个 QTL,但是,用已检测的 QTL 效应来调整表型观测值后,发现另外两个 QTL,这被其他独立实验所证实。这说明统计方法的合理利用可挖掘出更多的潜在信息。不过,这只是对连锁信息的巧妙利用,只是将单 QTL 模型拓展到多 QTL 模型。实际上,连锁不平衡信息也是可供利用的。Bodmer 最早提出用连锁不平衡进行 QTL 的精细定位。由于不构建分离群体和解析度较高等原因,它在人类复杂疾病的 QTL 定位研究中应用相当广泛。但是,在作物 QTL 定位中应用较少。不过,近年来日益受到重视,我国学者在水稻和小麦方面进行了探索。它的精度取决于研究群体的连锁不平衡的结构,群体中分布不均的等位基因亚群往往会导致较高的假阳性。例如,复杂的育种历史和野生种间有限基因流动造成了种质资源内的复杂分层,这使关联分析复杂化。幸运的是,Pritchard 等人结合群体结构估计与关联分析而提出的新方法及 Yu 等人提出的混合模型方法克服了该缺点,前者已应用于玉米开花时间基因 Dwarf8 的定位。当然,将连锁不平衡与连锁信息联合,精度会更高。若 QTL 区间存在候选基因,就可直接利用它进行基因的关联分析或互补检验。这种方法已在玉米研究中应用。 在增加重组机会方面,目前有几种策略:高代互交系(advanced intercross line,AIL)、选择表型(selective phenotyping)、轮回选择与回交系(recurrent selection and backcross,RSB)、高代回交系(advanced backcross line,ABL)、育成品种群体等。AIL 是通过 Ft-1 代两两个体间相互杂交使重组率增加,以提高 QTL 定位精度,如血浆胆固醇浓度 QTL 精细定位。若只选择分离群体中对 QTL 定位信息量大的重组个体,显然会使重组频率增加,这就是选择表型的思想。Jannink 通过计算机模拟证实了两种选择方案的优越性。Weight 认为,大效应的 QTL 可通过轮回回交与选择来积累紧密连锁座位间的重组,即 QTL 及其附近区域在不同系间仍保持分离,其他区域趋近轮回亲本。这就是 RSB。后来,Hill 获得了在 RSB 中对非轮回亲本表型进行定向选择后的 QTL 频率。最近,Luo 等人构建了 RSB 的 QTL 精细作图的理论方法,并已精细定位并克隆了酵母乙醇耐受性的主效基因 ASG1。ABL 就是没有实施选择的 RSB,为作物 QTL 精细定位的常用策略,已用于精细定位番茄果重 QTL。Li 等人将 ABL 与选择表型相结合,提出了相应的 QTL 定位方法。众所周知,新品种的培育是育种家有意识地重组优良基因的过程,说明由育成品种构成群体的重组频率比较高,因而可用来高解析地定位 QTL。这为Zhang 等人的结果所证实。 利用次级分离群体也是 QTL 精细定位的主要手段之一。它已应用于水稻抽穗期、分蘖角度、矮秆、油菜芥酸等性状的 QTL 精细定位。可以发现,这些研究都采用了大样本和目标区段高密度分子标记图谱,不过,对重组个体的大样本后裔鉴定有时也是重要的。为节约费用,可用分离亚群体,其精度也比较高。利用次级分离群体的技术关键是:(i)构建稳定的突变体或单 QTL 的近等基因系或染色体单片段的代换系(或渗入系)。不过,构建近等基因系的方法与 QTL 效应大小有关。常用的方法是用高代回交法。但是,当 QTL 效应较大时,也可直接在同一群体相同家系内中选择 QTL 近等基因系,还可节约时间;(ii)获得近等基因系(或代换系)与野生型杂交的分离群体;(iii)获得目标区间与目标基因紧密连锁的分子标记。若目标区段的 DNA 序列已知,如有大量的 EST 或 BAC 的 DNA 序列,设计新的 SSR 标记是容易的。此外,若有大量可供利用的染色体片段缺失系,通过互补检验也可精细定位 QTL。这时,需要个体数较少。 由于水稻等 DNA 全序列测定的完成,在目标区间寻找控制目标性状的候选基因应当是不难的。这为数量性状基因研究进入分子水平奠定了基础。 3 动态性状的 QTL 定位 动态性状是生物体在生长发育过程中随时间变化的数量性状,也称为发育性状、无限维特征、函数值性状和纵向性状等。动态性状 QTL 定位方法一般分3类:(i)将不同时间点表型观测值(或时间间隔表型观测值增量)视为相同性状的重复测定值,在重复观测值框架下依次分析该性状;(ii)将不同时间点观测值视为不同性状,由多变量方法分析该性状;(iii)拟合时间点与表型观测值的数学模型,用多变量方法分析模型参数。 第1类方法最简单。用常规的 QTL 定位方法分别分析不同时间点的资料,在不同时间点上定位了控制水稻分蘖数,松树苗直径、株高和体积以及老鼠体重的若干 QTL,揭示出不同发育阶段可能存在不同的基因。同时,若用 Zhu 提出的条件 QTL 定位方法分析两时间点的净效应时,其结果也是相似的。因而,用第1类方法分析动态性状可能不是最优的,可采用多性状 QTL 定位方法,即第2类方法。不过。随着观测时间点数的增加,变量维数和参数个数都会增加,增加了计算载荷。因而该方法适合于时间点数较少的情形。但是,若时间点数少。往往又不能准确地刻划性状动态变化过程。为减少变量维数,可用主成分方法获得主要的综合变量。但是,多个时间点表型观测值的线性组合(综合变量)的生物学意义有时是不清的。我们知道,随着时间点的增加,表型观测值与时间的曲线可能是一平滑曲线,该曲线可用生长曲线等数学模型来描述。因此,利用生长曲线等数学模型来拟合表型观测值与时间的关系,并对有生物学意义的模型参数进行多性状 QTL 定位便具有实际生物学意义。在这个意义上说,第3类方法是最优的。在实际应用中,最先使用的是两步法:先拟合数学模型,再以模型参数为依变量进行多性状 QTL 定位。利用该方法已定位了水稻叶龄动态性状的 QTL。与第2类方法相比,有一些优点:表型数据量减少,减轻了计算载荷;可处理非平衡数据;由于模型参数具有生物学意义,从而更能理解性状发育的遗传学基础。其不足之处是,没有考虑数学模型参数的估计误差。由此,Wu 等人将两步法改为一步法。迄今为止,已考虑的数学模型主要有:生长模型、正交多项式和异速生长模型。Wu 和 Li 认为,基于模型选择的 QTL 定位方法和 Bayesian 压缩估计方法均可用于动态性状的功能定位。 4 展望 4.1 种质资源新基因发掘的 QTL 定位方法 作物 QTL 定位群体一般是两纯合近交系的杂交后代,往往要求两近交系间差异较大。但是,若两者携带相同等位基因,即使其效应较大,也不能被检测到。因而,增加亲本数目的四向杂交甚至八向杂交就被提出。不过,其亲本数目也十分有限。而且,新基因是蕴藏在种质资源中的。因而,利用统计方法从大量种质资源中寻找新基因就是统计遗传学家的一大任务。目前,这方面的统计方法还不够成熟,需要进一步研究。它主要包括关联分析、“in silico”方法和基于 IBD 的混合模型方法。关联分析已在前面讨论,这里只介绍后两种方法。 Grupe 等人提出了一种“in silico”QTL 定位方法,在15个近交系组成的群体中定位了老鼠疾病相关性状的多个 QTL。它主要是通过数量性状表型距离与标记遗传型距离的相关分析预测 QTL 与标记间的连锁关系。若相关显著,说明该标记与 QTL 连锁。其中,数量性状表型距离是两纯系(品种)表型观测值之差;标记遗传型距离定义为:若两纯系 SNP 的单倍型 (haplotype) 相同,遗传型距离为0;否则为1。然而,Chesler 等人不能重复 Grupe 等人的结果,且功效低和假阳性率高。Darvasi 等人认为,在理想条件下检测遗传率为5%~20%的 QTL 时,需要纯合系40~150个;假阳性率太高,导致检测到的 QTL 需要用常规 QTL 定位方法予以验证。因而,该方法还需要进一步研究。 若利用大量育成纯合品种数量性状表型观测值、分子标记和品种间系谱关系,也可高解析定位 QTL,并且这些信息可用于品种分子设计育种。该方法的主要思想是利用品种的系谱关系计算品种间的后裔同样(identity by descent,IBD)值,并将 IBD 值嵌入方差组分模型以定位 QTL 的位置与效应;然后,用最优线性无偏预测(best linear unbiased prediction,BLUP)法预测出各品种的 QTL 效应值。根据每一品种各 QTL 效应预测值,可进行新品种的亲本选配和分子设计育种,也可研究基因在品种中的传递规律。Zhang 等人应用该方法定位了玉米 GDUSHD (growing degree day heat units to pollen shedding)的8个 QTL,误差变异系数仅为1.5%,QTL 定位的置信区间也较小。这些结果都说明其精度较高。 我国有丰富的品种资源,只要获得更多的相关信息,就可发掘出大量的有利基因并预测其遗传效应,进行分子设计育种,提高育种效率。 4.2 eQTL 定位的统计方法 表达谱数据分析通常是通过比较两个或多个处理间表达谱的差异以发掘与处理有关的基因;连锁遗传分析是检测分离群体中标记与性状间的连锁。显然,分离群体所有个体的表达谱使得让每一基因的表达谱作为一个性状成为可能,将表达谱作为数量性状所定位得到的 QTL 称为 eQTL。当 eQTL 的遗传连锁与该基因的位置一致时,便可确定与数量性状有关的基因。这就是 Jansen 和 Nap 提出的 eQTL 定位的基本思想,并在酵母、玉米和老鼠等中得以应用。与此不同的是,Hoti 和 4.3 遗传交配设计的 QTL 定位方法 从作物 QTL 定位群体来看,主要是针对简单的分离群体,如 F2,BC(backcross),DH(double haploid),RIL frecombinant inbred line) 和 AIL 等,所涉及的亲本较少。但是,从数量遗传学发展历程可知,遗传交配设计对数量遗传学有很大的贡献。因此,研究基于遗传交配设计的 QTL 定位方法也是应当重视的。最近,Verhoeven 等人通过 QTL 定位方法检测双列杂交设计的 QTL,并通过双列杂交遗传分析确定研究多基因遗传模式的新方法;我国学者提出利用随机交配群体来无偏估计胚乳性状 QTL 的第一和第二显性效应。然而,这方面的研究还相当薄弱,需要进一步探索。 4.4 生活力基因定位方法 由于生活力基因影响其附近分子标记的分离比例,故可通过分子标记偏分离来检测生活力基因。一般的方法是获得它的选择系数、显性度和与标记的重组率,还可间接获得其基因型频率。然而,不能提供其遗传效应估计值。这对阐明进化机制是不利的。其主要原因是没有表型观测值。最近,Luo 等人考虑了一种假想性状(liability)受生活力基因控制,它对研究者来说是不可见的,但是,对自然来说是可见的。由此,可用 QTL 定位方法来定位生活力基因,并获得其遗传效应估计值,为遗传进化研究提供一种新方法。Nichols 也给出了一个很好的评论。利用该模型,我们研究了标记偏分离对标记间遗传距离估计值的影响,认为偏分离一般会低估标记间遗传距离,只有在特定遗传模式下会高估之。但是,其偏性可被矫正。今后,这方面还有很多工作要做。 总之,有关数量性状基因研究将不断深入,新方法与新技术将不断出现。例如,在稀有疾病研究中,连锁定位精度受到可利用减数分裂数和有信息标记密度的限制,但是,SNP 标记的出现就克服了这些缺点,以便精细定位 QTN (quantitative trait nucleotide)。毫无疑问,本文未囊括所有 QTL 定位方法的进展。尽管多性状 QTL 定位有高的功效且能研究一因多效,但是,本文未予综述。 注: (浏览次数:)
|
| 上篇文章:植物转脂蛋白的抗病机制研究进展 |
| 下篇文章:microRNA 及其在植物生长发育中的作用 |
| 推荐给朋友 | 打印 | 关闭窗口 |
| 相关文章: |
| 友情链接: |
|
| Copyright © 2003 CNRRI. All rights reserved. 中国水稻研究所 版权所有 地址:杭州市体育场路359号(邮政编码:310006)  |